Convolution of waveforms using Python compared to MATLAB
We will see compare the convolution functions in Python (Numpy) with the conv function in MATLAB. If you have tried them both then you would know that its not exactly same.
We will see compare the convolution functions in Python (Numpy or Scipy) with the conv function in MATLAB. If you have tried them both then you would know that its not exactly same. In the end we will try to find how can we make the Python convolution works in the same way as the MATLAB one. This can be helpful in translating the code from MATLAB to Python.
Convolution
Convolution is a mathematical operation on two functions (\(f\) and \(g\)) that produces a third function \( conv \) that expresses how the shape of one is modified by the other. It is defined as the integral of the product of the two functions after one is reversed and shifted.
\begin{equation} f * g (t) = \int_{-\infty}^{\infty} f(\tau) g(t-\tau) d\tau \end{equation}
We have seen several posts about the cross-correlation. Convolution can be seen as the cross-correlation of \(f(x)\) and \(g(-x)\), or \(f(-x)\) and \(g(x)\) for the real-valued functions. For the complex valued functions, the cross-correlation operator is the adjoint of the convolution operator.
1-D convolution analytical example
Let us take two arrays:
f = [1, 2, 3]
g = [5, 6, 7]
Now, let us compute the convolution of the two arrays step by step:
- Reverse the function \(g\) for the \(f*g\).
f = [1, 2, 3] g_ = [7, 6, 5] - Now, we compute the convolution at
t = 0f = [_, _, 1, 2, 3] g_ = [7, 6, 5, 0, 0] prod0 = [_, _, 5, 0, 0] = 5 - Then, we compute the convolution at
t = 1f = [_, 1, 2, 3] g_ = [7, 6, 5, 0] prod1 = [_, 6, 10, 0] = 16 - Then, we compute the convolution at
t = 2f = [1, 2, 3] g_ = [7, 6, 5] prod2 = [7, 12, 15] = 34 - Then, we compute the convolution at
t = 3f = [1, 2, 3, _] g_ = [0, 7, 6, 5] prod3 = [0, 14, 18, _] = 32 - Then, we compute the convolution at
t = 4f = [1, 2, 3, _] g_ = [_, 0, 7, 6] prod3 = [_, 0, 21, _] = 21
So, we got the convolution to be: [5, 16, 34, 32, 21].
Convolution using Python
Using the mode full
Python
import numpy as np
f = [1, 2, 3]
g = [5, 6, 7]
conv1 = np.convolve(f,g,'full')
print(conv1)
$ [ 5 16 34 32 21]
MATLAB
clear all; close all; clc;
f = [1 2 3];
g = [5 6 7];
fgconv = conv(f,g,'full')
fgconv =
5 16 34 32 21
Using the mode same
This returns the output of the length same as the max(len(f), len(g)).
Python
import numpy as np
f = [1, 2, 3]
g = [5, 6, 7]
conv1 = np.convolve(f,g,'same')
print(conv1)
$ [16 34 32]
MATLAB
clear all; close all; clc;
f = [1 2 3];
g = [5 6 7];
fgconv = conv(f,g,'same')
fgconv =
16 34 32
Using the mode valid
The convolution product is only given for points where the signals overlap completely.
Python
import numpy as np
f = [1, 2, 3]
g = [5, 6, 7]
conv1 = np.convolve(f,g,'valid')
print(conv1)
$ [34]
MATLAB
clear all; close all; clc;
f = [1 2 3];
g = [5 6 7];
fgconv = conv(f,g,'valid')
fgconv =
34
Convolution of signals of different lengths
Now, let us consider a case where the length of the two arrays differs for the mode same. It is as we can expect, same for the full and valid mode. Let us first compute the covolution in Python using the same approach.
Python
import numpy as np
f = [-1, 2, 3, -2, 0, 1, 2]
g = [2, 4, -1, 1]
conv1 = np.convolve(f,g,'same')
print(conv1)
$ [ 0 15 5 -9 7 6 7]
MATLAB
clear all; close all; clc;
f = [-1 2 3 -2 0 1 2];
g = [2 4 -1 1];
fgconv = conv(f,g,'same')
fgconv =
15 5 -9 7 6 7 -1
This post explains the reason behind this.
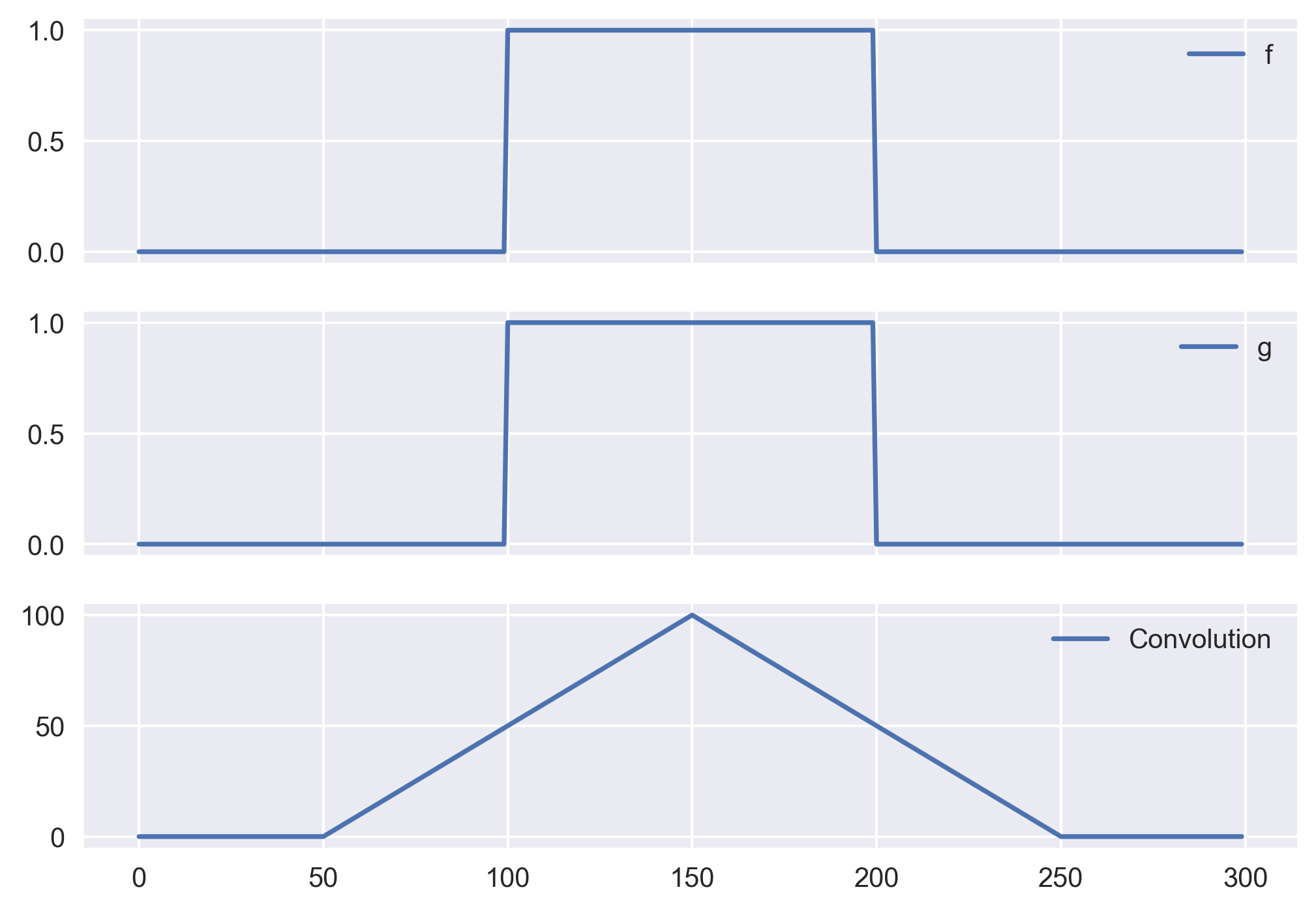
Convolution of two signals
Let us take two heaviside functions and compute the convolution of the two. Note that in this case, the convolution is same as the correlation because the function g is even function (\(g(\tau) = g(-\tau)\)).
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
plt.style.use('seaborn')
sig1 = np.repeat([0., 1., 0.], 100)
sig2 = np.repeat([0., 1., 0.], 100)
filtered = np.convolve(sig1, sig2, mode='same')
fig, ax = plt.subplots(3,1, sharex=True)
ax[0].plot(sig1, label='f')
ax[1].plot(sig2, label='g')
ax[2].plot(filtered, label = 'Convolution')
for axx in ax:
axx.legend()
plt.savefig('convolvesigs.png',bbox_inches='tight', dpi=300)
Conclusions
So, we can conclude that the Python and MATLAB implementation of the convolution function results same output when the length of the two arrays is same. However, when the length of the two arrays is not same, then the way MATLAB does the padding is slightly different than that of Python for the mode where we output the arrays of the same length as the minimum length of the arrays.
Disclaimer of liability
The information provided by the Earth Inversion is made available for educational purposes only.
Whilst we endeavor to keep the information up-to-date and correct. Earth Inversion makes no representations or warranties of any kind, express or implied about the completeness, accuracy, reliability, suitability or availability with respect to the website or the information, products, services or related graphics content on the website for any purpose.
UNDER NO CIRCUMSTANCE SHALL WE HAVE ANY LIABILITY TO YOU FOR ANY LOSS OR DAMAGE OF ANY KIND INCURRED AS A RESULT OF THE USE OF THE SITE OR RELIANCE ON ANY INFORMATION PROVIDED ON THE SITE. ANY RELIANCE YOU PLACED ON SUCH MATERIAL IS THEREFORE STRICTLY AT YOUR OWN RISK.