Non-linear curve fitting to a model with multiple observational variables in MATLAB (codes included)
How to fit data to non-linear model
Non-linear model is the one in which observational data is modeled by a non-linear combination of one or more model parameters and observational variables.
The non-linear equation is of the form:
\[y = f(x1,x2)\]In this case, we use the MATLAB function lsqcurvefit:

%% Fit Model
% - Utpal Kumar
clear; close all; clc
% generate some random data
Kdp = 0:40;
Zdr = 100:100+length(Kdp)-1;
xdata = [Kdp; Zdr]; %define independent variable
noise = 0.1*randn(size(xdata(1,:)));
ydata = 26.778*xdata(1,:).^0.946 .*xdata(2,:).^-1.249 + noise; %define dependent, ydata
% define optimization options
options = optimset('Display','iter','FunValCheck','on', ...
'MaxFunEvals',Inf,'MaxIter',Inf, ...
'TolFun',1e-6,'TolX',1e-6);
paramslb = [-Inf -Inf -Inf]; % lower bound
paramsub = [ Inf Inf Inf]; % upper bound
% define the initial seed
params0 = [20,0.9,-1.2];
% define model function
modelfun = @(pp,xdata) pp(1)*xdata(1,:).^pp(2).*xdata(2,:).^pp(3);
[params,resnorm,residual,exitflag,output] = lsqcurvefit(modelfun,params0,xdata,ydata,paramslb,paramsub,options);
params
% compute model fit
modelfit = modelfun(params,xdata);
% check squared error (the aim is to minimize squared error)
squarederror = sum((ydata(:)-modelfit(:)).^2)
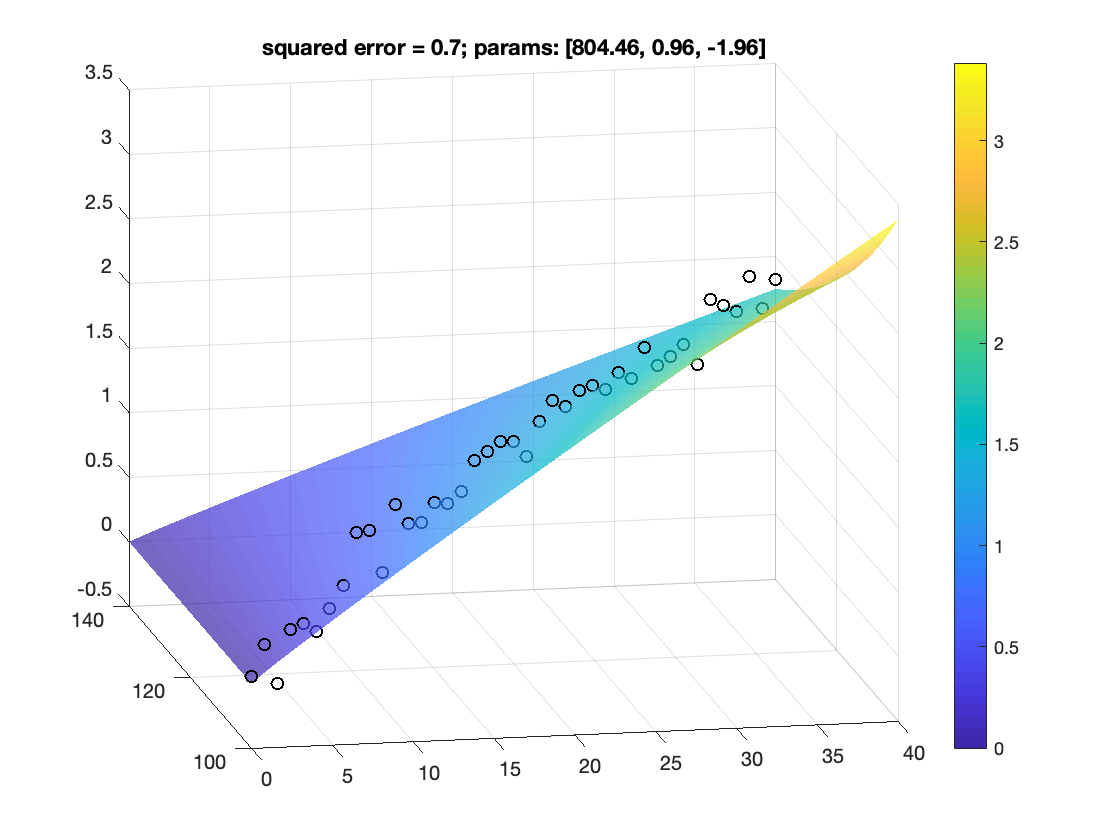
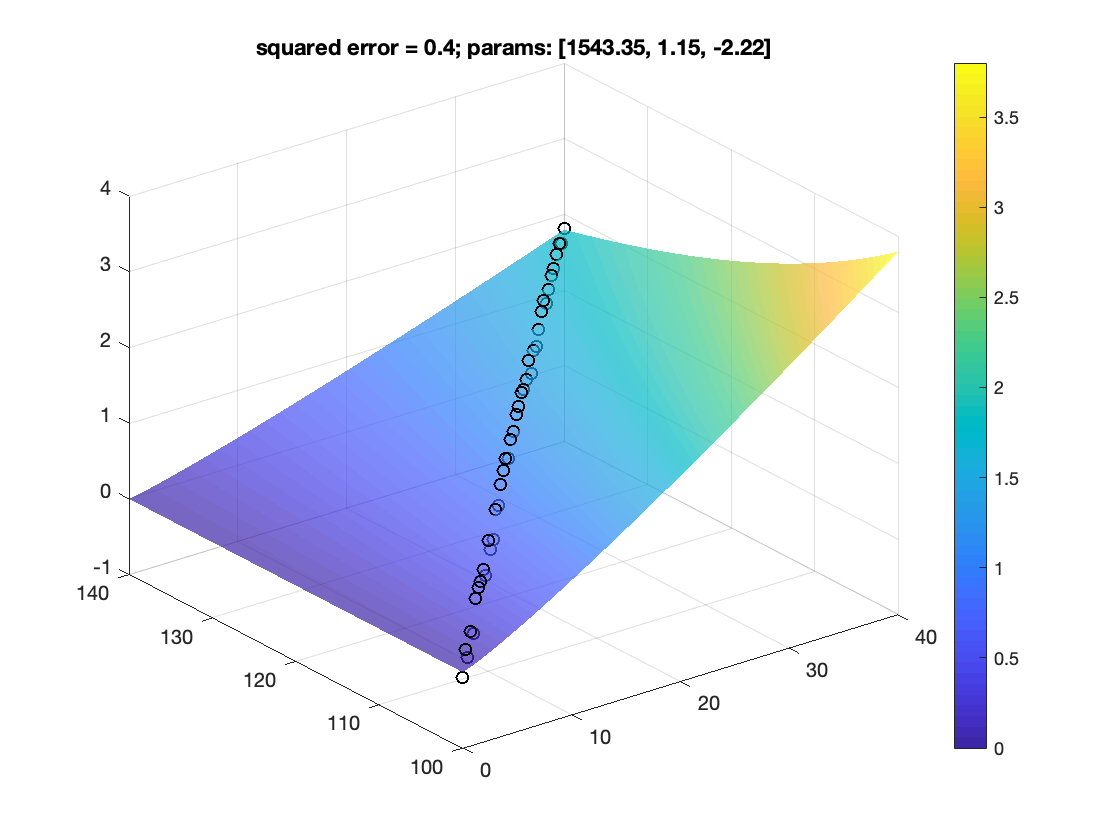
% visualize the data and results
figure;
scatter3(xdata(1,:),xdata(2,:),ydata,'k') %scatter plot of data
hold on
[X,Y] = meshgrid(xdata(1,:),xdata(2,:));
Z = params(1)*X.^params(2) .*Y.^params(3);
s = surf(X,Y,Z,'FaceColor','interp','FaceAlpha',0.7); %surface plot of the results with the estimated parameters
s.EdgeColor = 'none';
colorbar
title(sprintf('squared error = %.1f; params: [%.2f, %.2f, %.2f]',squarederror,params(1),params(2),params(3)));
OUTPUT:
Norm of First-order
Iteration Func-count f(x) step optimality
0 4 3.00771 45.8
1 8 1.01784 10 18.5
2 12 1.01784 20 18.5
3 16 0.749083 5 3.19
4 20 0.749083 10 3.19
5 24 0.739709 2.5 0.941
6 28 0.736382 5 2.32
7 32 0.730617 5 2.06
8 36 0.725309 5 1.68
9 40 0.720793 5 1.39
10 44 0.716863 5 1.17
11 48 0.716863 10 1.17
12 52 0.714394 2.5 0.363
13 56 0.702756 5 1.61
14 60 0.702475 10 2.95
15 64 0.69606 2.5 0.302
16 68 0.692996 5 0.649
17 72 0.692936 10 2.11
18 76 0.689562 2.5 0.248
19 80 0.685872 5 1.03
20 84 0.684458 10 1.45
21 88 0.682476 10 1.15
22 92 0.680904 10 0.983
23 96 0.679528 10 0.849
24 100 0.678304 10 0.74
25 104 0.677204 10 0.649
26 108 0.677204 20 0.649
27 112 0.676476 5 0.188
28 116 0.675021 10 0.279
29 120 0.675021 20 0.279
30 124 0.674572 5 0.461
31 128 0.673816 10 0.439
32 132 0.673816 20 0.439
33 136 0.673347 5 0.165
34 140 0.666859 10 1.04
35 144 0.666859 20 1.04
36 148 0.66599 5 0.11
37 152 0.665912 10 0.313
38 156 0.665785 10 0.301
39 160 0.665663 10 0.278
40 164 0.665549 10 0.257
41 168 0.665443 10 0.238
42 172 0.665344 10 0.221
43 176 0.665251 10 0.206
44 180 0.665164 10 0.192
45 184 0.665082 10 0.18
46 188 0.665082 20 0.18
47 192 0.665025 5 0.0544
48 196 0.66496 10 0.135
49 200 0.66496 20 0.135
50 204 0.664915 5 0.0478
51 208 0.664852 10 0.117
52 212 0.664852 20 0.117
53 216 0.664813 5 0.043
54 220 0.664754 10 0.101
55 224 0.664754 20 0.101
56 228 0.664719 5 0.0385
57 232 0.664664 10 0.0868
58 236 0.664664 20 0.0868
59 240 0.664633 5 0.0342
60 244 0.664581 10 0.0722
61 248 0.664581 20 0.0722
62 252 0.664553 5 0.0296
63 256 0.664503 10 0.0543
64 260 0.664503 20 0.0543
65 264 0.664479 5 0.0227
66 268 0.664421 10 0.0334
67 272 0.664421 20 0.0334
68 276 0.664401 5 0.0725
69 280 0.664365 10 0.0896
70 284 0.664364 20 0.321
71 288 0.66428 5 0.0308
72 292 0.66425 10 0.0596
73 296 0.664243 20 0.273
74 300 0.664181 5 0.027
75 304 0.664156 10 0.0495
76 308 0.664146 20 0.235
77 312 0.6641 5 0.0237
78 316 0.664078 10 0.0421
79 320 0.664068 20 0.205
80 324 0.664032 5 0.0208
81 328 0.664015 10 0.0369
82 332 0.664006 20 0.181
83 336 0.663979 20 0.174
84 340 0.663953 20 0.163
85 344 0.663931 20 0.152
86 348 0.663912 20 0.143
87 352 0.663895 20 0.134
88 356 0.663881 20 0.126
89 360 0.66387 20 0.119
90 364 0.663861 20 0.112
91 368 0.663854 20 0.105
92 372 0.66385 20 0.0991
93 376 0.663847 19.0329 0.0845
94 380 0.663842 0.413735 2.64e-05
95 384 0.663842 0.0136481 3.46e-08
Local minimum found.
Optimization completed because the size of the gradient is less than
the selected value of the optimality tolerance.
<stopping criteria details>
params =
804.4592 0.9611 -1.9579
squarederror =
0.6638
Similar posts
Disclaimer of liability
The information provided by the Earth Inversion is made available for educational purposes only.
Whilst we endeavor to keep the information up-to-date and correct. Earth Inversion makes no representations or warranties of any kind, express or implied about the completeness, accuracy, reliability, suitability or availability with respect to the website or the information, products, services or related graphics content on the website for any purpose.
UNDER NO CIRCUMSTANCE SHALL WE HAVE ANY LIABILITY TO YOU FOR ANY LOSS OR DAMAGE OF ANY KIND INCURRED AS A RESULT OF THE USE OF THE SITE OR RELIANCE ON ANY INFORMATION PROVIDED ON THE SITE. ANY RELIANCE YOU PLACED ON SUCH MATERIAL IS THEREFORE STRICTLY AT YOUR OWN RISK.